For something a little bit different here is a link to the OpenRocket source download. It’s a Java based program. Don’t expect exact ballistics software but you cna construct your own designs and use the Component Analysis function to see how changes affect the drag etc.
So here is a link to download the original MS Excel spreadsheet for Nose Cone Design.
I use a modified version myself to plot shapes that resemble long range target projectiles. If I can do it I’m sure those of you some knowledge of spreadsheets can come up with their own modified version. Follow the instructions and enjoy!
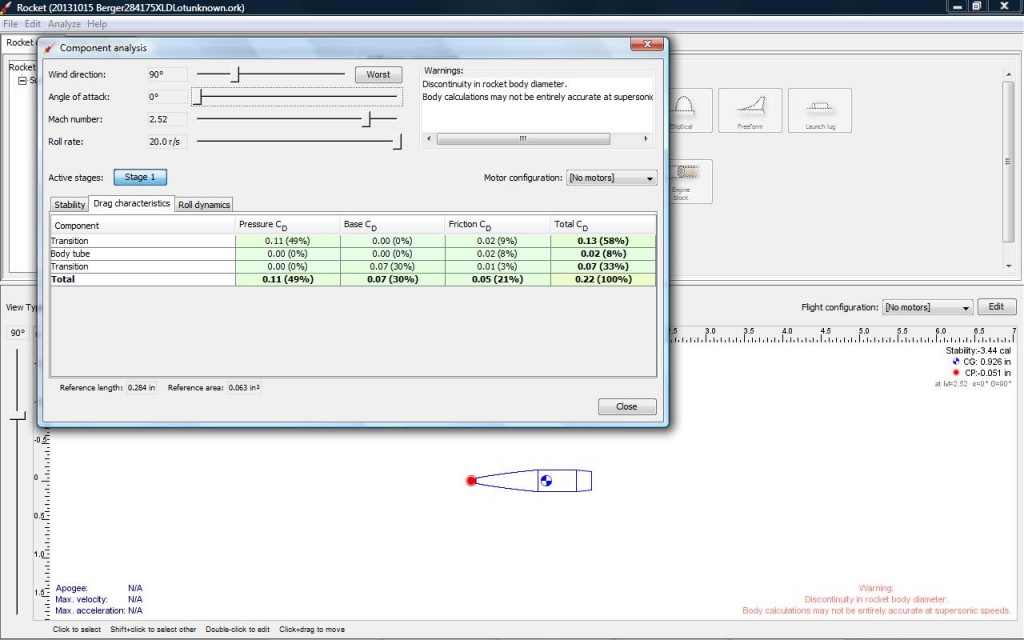
So if you’ve managed to magnify the outline of your ogive, effectively you can calculate the radius by measuring the meplat to the shank/ogive intersection. This will become your chord length W.
The Sagitta of the arc or height (H), is measured perpendicular from the midpoint of the chord W.
For double or multiple radius ogives there will be multiple chord lengths measure. Note also this method only works with ogives using a tangent and secant radius. The larger your outline is magnified the more accurate your measure will be, useful for those of us without an optical shadowgraph comparator or other such metrology equipment. Remember though you may have to contend with the parallax error depending on how you capture your image outline.
(link to Math Open Reference.)
Given an arc or segment with known width and height:
 |
where: W is the length of the chord defining the base of the arc H is the height measured at the midpoint of the arc’s base. |
